Paradoxes de la mesure de l'information
Par Jean-Michel Salaun le vendredi 11 février 2011, 05:44 - Sémio - Lien permanent
Le numéro de Science qui vient de sortir (ici) est entièrement consacré aux questions posées par l'explosion quantitative des flux de données pour la recherche. Les articles concernent autant les transformations sur des disciplines (climat, écologie, neuroscience, santé, sciences sociales, biologie, génomique, physique des particules, astrophysique..) que des problématiques transversales (visualisation 3D, théorisation des capteurs et du signal, métaconnaissances, mesure de l'information). Un numéro très riche donc, essentiel témoignant d'un tournant fondamental dans la construction et l'exposition de nos savoirs.
Avant de présenter dans un futur billet un article particulièrement stimulant sur le traitement des métaconnaissances dans les articles scientifiques (ici), je voudrais alerter sur les interprétations trop rapides que l'on peut faire d'un autre.
Martin Hilbert et Priscilla Lopez, “The World's Technological Capacity to Store, Communicate, and Compute Information,” Science Express (Février 11, 2011): 692-693. (là)
Celui-ci reprend un leitmotiv des sciences de l'information : la mesure de l'explosion de l'information. Sans surprise car il fait image et paraît illustrer ou même démontrer scientifiquement d'une situation que chacun pressent, il a déjà été largement signalé et commenté par la presse (par ex ici, là, là, ou pour être en résonance avec mon sujet là). Il tente, en effet, de mesurer l'information enregistrée, l'information communiquée et l'activité de calcul. Ici je ne reprendrai que le raisonnement concernant l'information enregistrée.
L'ensemble peut-être résumé par cette diapo et trois citations :
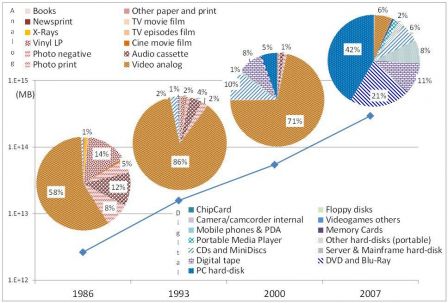
Extraits (trad JMS) :
Le montant total d'information s'est accru de 2,6 exaoctets (10 puissance 20) compressés de façon optimale en 1986 à 15,6 en 1993, plus de 54,5 en 2000, à 295 en 2007. C'est l'équivalent de pas moins d'un cédérom de 730 Mo par personne en 1986 (539 Mo), en gros 4 cédéroms par personne en 1993, 12 l'année 2000 et presque 61 en 2007. (..)
En 1986, les disques vinyles comptaient encore pour une part significative (14%), tout comme les cassettes audio analogiques (12%) et la photo (5 et 8%). Ce n'est qu'à partir de 2000 que le numérique a commencé à compter pour notre mémoire technologique, représentant 25% du total. Les disques durs se taillent la part du lion en 2007 (52%), les disques optiques font plus du quart (28%) et les bandes numériques environ 11%. Les solutions de stockage sur papier prennent une part décroissante (0,33% en 1986 et 0,007% en 2007), bien que leur capacité n'a pas cessé d'augmenter en terme absolu de 8,7 à 19,4 Petaoctets compressés de façon optimale.
Si leur démonstration me parait bien illustrer la rapidité de la bascule vers le numérique, elle pose une question préalable quant à l'étalon de mesure et donc son interprétation. Voici donc les éléments à ce sujet, qu'on ne retrouve malheureusement pas dans les comte-rendus de presse :
L'information dans sa conception théorique est l'opposée de l'incertitude. Shannon a défini un octet comme la quantité d'information qui réduisait l'incertitude de moitié (dans un espace de probabilité comme des lettres de l'alphabet ou des pixels sur une échelle de couleur). Cette définition est indépendante de la tâche spécifique ou du contenu. Après normalisation en octets compressés nous pouvons dire par exemple « une image de journal carrée de 6cm de côté est équivalente à 1.000 mots », parce que les deux demandent le même nombre moyen de décisions binaires oui/non pour résoudre le même montant d'incertitude.
Cet étalon est classique, c'est celui de la théorie générale de l'information de Shannon (wkp). Il a déjà été beaucoup discuté, car il fait référence à concept d'information particulier, qui sert à l'optimisation du signal. Certains, notamment Weaver par la cybernétique, ont voulu l'étendre à toute situation de communication, non sans ambiguïtés (wkp). Mais s'il est dans cet article cohérent de l'employer pour mesurer les capacités de stockage informatique, cela devient plus problématique lorsque que l'on déborde sur d'autres domaines et la polysémie du mot information nous fait vite déraper. Les auteurs de l'article ne manquent pas de tomber dans ce travers.
Même en restant dans la perspective mécaniste qui est la leur, deux objections viennent rapidement à l'esprit :
- Mesurer l'information contenue sur un support analogique avec un étalon numérique préjuge déjà que l'ensemble de celle-ci sera converti en numérique. Supposons un instant que nous fassions l'inverse, mesurer l'information numérique par un étalon papier, c'est à dire tout simplement mesurer la surface de la sortie imprimante ramenée à un format moyen (comme les auteurs ont pris une compression optimale pour le signal). Nous aurions alors approximativement le résultat suivant pour le même exemple : « une image de journal carrée de 6cm de côté est équivalente à 76 mots » avec une mesure indépendante de la tâche spécifique ou du contenu. Le rapport quantitatif entre l'image et l'écrit est totalement inversé.
- Plus problématique encore, les auteurs concluent leur article par une comparaison entre la capacité humaine à traiter l'information par les neurones et la capacité des ordinateurs. Mais nous savons aujourd'hui la captation et le traitement du signal par les sens et un cerveau humain pour la lecture par exemple (wkp), n'a pas grand chose à voir avec celle d'un ordinateur. Et que penser de l'image vidéo à 25 images par seconde, traitée à l'évidence complètement différemment par l'œil humain, la persistance rétinienne et notre cerveau, et par un signal numérique et un ordinateur analysant séparément chaque image ?
Dès lors que mesurent vraiment les auteurs de l'article ?
Actu du 15 février
Voilà un bel exemple de ce que devient l'étude revisitée par la presse, et réduite à un schéma sans référence à la pertinence de la mesure ici le Washington Post